我们时常看到文章中有基因共表达网络图片，其实大部分基因网络分析的方法，都与基因间表达量相关系数的计算相关。例如，通过计算不同基因表达量的相关系数，来构建基因共表达网络。所以理解相关系数，对分析生物学数据非常重要。

相关表和相关图可反映两个变量之间的相互关系及其相关方向，但无法确切地表明两个变量之间相关的程度。于是统计学家设计了统计指标——相关系数。

相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算，同样以两变量与各自平均值的离差为基础，通过两个离差相乘来反映两变量之间相关程度。
这里，我们就来谈谈基因共表达分析中最常用的两种相关系数：皮尔森相关系数（Pearson correlation coefficient）与斯皮尔曼等级相关（Spearman’s correlation coefficient for ranked data）系数。

皮尔森相关系数
在所有相关系数的计算方法里面，最常见的就是皮尔森相关。皮尔森相关系数也称皮尔森积差相关系数，是一种线性相关系数。皮尔森相关系数是用来反映两个变量线性相关程度的统计量。相关系数用r表示，其中n为样本量，Xi Yi与 分别为两个变量的观测值和均值。r描述的是两个变量间线性相关强弱的程度。r的绝对值越大表明相关性越强。SX SY分别为样本标准差。

假设样本可以记为(Xi ，Yi)，则样本Pearson相关系数为：

公式是抽象的，我们利用几组值就可以更好理解相关系数的意义。从皮尔森相关系数定义来看，如果两个基因的表达量呈线性关系（数学上，线性相关指的是直线相关，指数、幂函数、正弦函数等曲线相关不属于线性相关），那么两个基因表达量的就有显著的皮尔森相关系性。下面用几组模拟数值来测试一下：

1、测试1
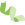
两个基因A、B，他们的表达量关系是B=2A，在8个样本中的表达量值如下：
表1 基因A、B在8个样本中的表达量值

图1 基因A、B在8个样本中的表达量示意图

计算得出，他们的皮尔森相关系数r=1，P-vlaue≈0。

2、测试2
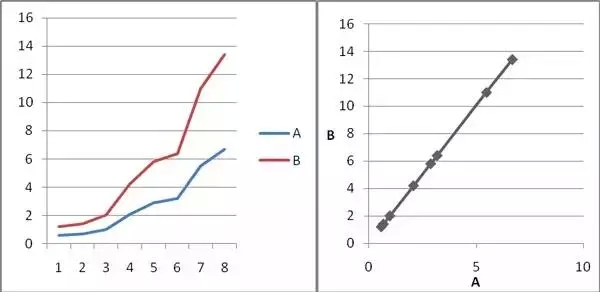
两个基因A、C，他们的关系是C=15-2A，在8个样本中的表达量值如下：
表2 基因A、C在8个样本中的表达量值

图2基因A、C在8个样本中的表达量示意图

计算得出，他们的皮尔森相关系数r=-1，P-vlaue≈0。

从以上可以直观看出，如果两个基因的表达量呈线性关系，则具有显著的皮尔森相关性。如果两个基因“共舞”（如图1），则两者正相关；相反如图2，则两者负相关。
以上是两个基因呈线性关系的结果。如果两者呈非线性关系，例如幂函数关系（曲线关系），下面也用模拟数值来测试一下。

3、测试3
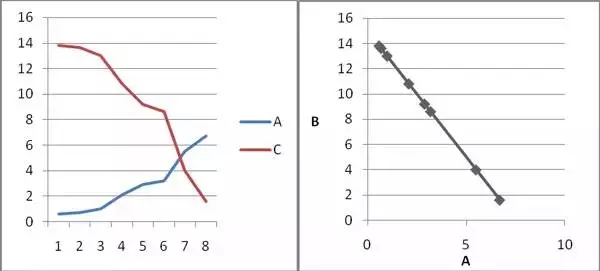
两个基因A、D，他们的关系是D=A10，在8个样本中的表达量值如下：
表3 基因A、C在8个样本中的表达量值

图3基因A、C在8个样本中的表达量示意图

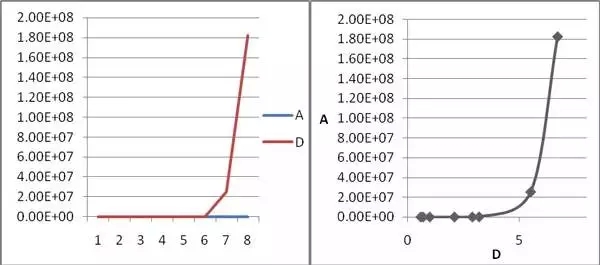
计算得出，他们的皮尔森相关系数等于 0.77，P value= 0.0267。

可以看到，基因A、D相关系数，无论数值还是显著性都下降了。皮尔森相关系数是一种线性相关系数，因此如果两个变量呈线性关系的时候，具有最大的显著性。对于非线性关系（例如A、D的幂函数关系），则其对相关性的检测功效会下降。但在生物体内的许多调控关系，例如转录因子与靶基因、小干扰RNA与靶基因，可能都是非线性关系，这时可以考虑另外一个相关系数计算方法：斯皮尔曼等级相关。

关联阅读：相关系数（二）：斯皮尔曼等级相关

更多基迪奥精彩原创文章，可继续关注我们网站动态发布，同时关注基迪奥微信~扫一扫添加基迪奥好友~随时随地关注行业动态！